Derived Quantities

Delivered Quantities

Delivered quantity is the quantity which obtained from physical quantity. It includes

i)     Area

ii)    Volume

iii)   Density

iv)  Weight

v)   Speed

vi)  Velocity

vii) Force

viii)     Pressure

Delivered Quantity and Their Si Unit

Quantities	SI-Unit	Unit Symbol
Area	Square metre	m2
Volume	Cubic metre	m3
Density	Kilogram per Cubic metre	Kg/m3
Weight	Newton	N
Speed	Metre per second	m/s
Velocity	Metre per second	m/s
Force	Newton	N
Pressure	Newton per Square metre	N/m2

Weight 

Weight is the force of gravity acting on an object? SI unit of weight is Newton (N). It is measured by spring balance. It is varying with position  

Mathematically:

W = mg

Where:

W = weight

M = mass

g = Acceleration due to gravity (Gravitation force)

Difference between Mass and Weight

Mass	Weight
Is the quantity of matter in an object	Is a force of gravity on an object
It is constant	It varies with environment
It is a fundamental quantity	It is a derived quantity
Its SI unit is kilogram (kg)	Its SI unit is Newton (N)
It is measured by beam balance	It is measured by spring balance
Is a scalar quantity	Is a vector quantity

NB:

The gravitation force on the Earth’s surface is higher than the gravitation force on the moon’s surface, that’s why objects weigh more on the Earth than when on moon.

$$~~~~~~~~~~~~~~~~~~~~~~~~~~~~\ Gravitation force on the Moon = \frac{1}{6} \times (Gravitation force on the Earth)$$ $$\\\qquad~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~\ g_m = \frac{1}{6} \times g_e$$

Example

What would be the weight Astronomer of 72 Kg when is on the;

a)   Earth’s surface

b)   Moon’s surface

(Acceleration due to gravity = 10 m/s²)

Solution

Data given

Mass (m) = 72 kg

Acceleration due to gravity on the Earth (g_e) = 10 m/s²

Weight on Earth (W_e) =?

Weight on Moon (W_m) =?

a)   Earth’s surface

$$\\\qquad~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~W = mg$$ $$\\\qquad~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~W_e = m \times g_e$$ $$\\\qquad~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ = 72 \times 10$$ $$\\\qquad~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ = 720~N$$

The weight of the Astronomer when is on the Earth Surface = 720 N

b)   Moon’s surface

$$\\\qquad~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~W = mg$$ $$\\\qquad~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~W_m = m \times g_m$$ $$\\\qquad~~~~~~~~~~~~~~~But~~~~~g_m = \frac{1}{6} \times g_e$$ $$\\\qquad~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~W_m = m \times \frac{1}{6} \times g_e$$ $$\\\qquad~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ = 72 \times \frac{1}{6} \times 10$$ $$\\\qquad~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ = 12 \times 10$$ $$\\\qquad~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ = 120~N$$

The weight of the Astronomer when is on the Moon's Surface = 120 N

Volume

Volume is the quantity of space that an object occupies. Si unit of volume is

cubic metre (m³)

NB:

Other unity obtains from the cubic metre, namely

i)     Cubic Kilometer (km³)

ii)    Cubic Centimeter (cm³)

iii)   Cubic decimeter (dm3)

iv)  Millilitre (ml)

v)   Litre (l)

Their equivalent is as follows

i)     1l = 1000 cm³

ii)    1l = 1000 mL

iii)   1L = 1dm³

Volume of Solid Regular Object

Regular object is the object with known shape. For Example, cylinder, rectangular, cube etc. The volume of regular object is obtained by formula

Formula of Volume

Volume of object is obtained by multiplication of area (A) of regular object and height (h) of regular object

V = A x h

Where:

A = area of regular object

h = height of regular object

Volume of Cube Object

Diagram:

Formula: V = A x h 

Then: v = l x w x h

Where:

V = volume

l = length of cube

h = height of cube

w = width of cube

But: for cube l = h = w

$$Volume~~of~~Cuboid= Length \times Length \times Length$$

Volume of Rectangular Object

Diagram:

Formula: v = A x h 

Then: v = l x w x h

$$Volume~~of~~Rectangular~~block= Length \times Width \times Height$$

Volume of Cylinder Object

Diagram:

Formula: v = A x h 

But A = πr²

Then V = πr²xh

Where:

V = volume

r = radius of object

h = height of object

$$Volume~~of~~cylinder= π r^2 h$$

Volume of Sphere Object (h = r)

Diagram:

$$Formula~~~~V= π r^2 h$$

Where:

V = volume

r = radius of sphere

$$Volume~~of~~Sphere= \frac {4π r^3} {3}$$

Example 1

Calculate the volume of rectangular block of sides 15cm, 8cm and 7cm

Solution

Data given:

Length of block (l) = 15cm

Breath of block (w) = 8cm

Height of block (h) = 7 cm

Volume of block, v =?

Solution:

v = l x b x h

   = 15 x 5 x 7

   = 840 cm³ 

The volume of rectangular block = 840 cm³ 

Example 2 

Calculate the volume of figure below given that π = 3.14

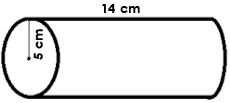
Solution

Data given:

Length of cylinder (l) = 14cm

Radius of cylinder (r) = 5cm

π = 3.14

V = πr²xh

    = 3.14 x 5 x 5 x 14

    = 1099 cm³

The volume of cylinder block = 1099 cm³

Volume of Liquid

Litre is the standard unit used for measuring the volume of liquids.

The instrument or apparatus used to measure volume of liquids include;

i)     Burette

ii)    Pipette

iii)   Volumetric flask

iv)  Measuring cylinder

Nb:

During measurement eye should be line with the meniscus of the liquid

Diagram:

Volume of Solid Irregular Object

Regular object is the object with unknown shape. For Example, stone, human body etc. The volume of irregular object is obtained by displacement method or immersion method

Displacement Method

Volume of irregular object is based on the principle that when an object is completely submerged in water it’s displacing a volume of water equal to its own volume. This done by;

i)     Graduated cylinder

ii)    Eureka can or overflow can

Graduated Cylinder

Suppose you want to measure the volume of a small stone. The following steps are necessary

i)     Fill graduated cylinder to known mark (let be 30ml)

ii)    Record the water volume i.e. 30ml as v₁

iii)   Gently drop the stone into the water

Diagram:

iv)  Record the new volume of water as v₂

Calculate the different in volume which is the volume of stone, v

$$V= V_2 - V_1$$

Example, 

When an irregular solid was immersed in 65cm³ of water the water level rises to 81cm³. What was the volume of the solid?

Solution

Data given

Initial volume (v₁) = 65cm³

Final volume (v₂) = 81cm³

Volume (v₁) =?

v = v₂ - v₁

                           = 81 – 86

                           = 16 cm³

The volume of the solid = 16 cm³

Eureka Can

If the object is large to fit into graduated cylinder, eureka can common known as an overflow can used. The following steps should be followed

i)     Fill the overflow can with water up to the level of the spout

Diagram:

ii)    Tie the irregular object with a string; gently drop the irregular object into water using string

iii)   The irregular object will displace some water which will be collected in the beaker

Diagram:

iv)  Transfer the displaced water into a graduated cylinder

v)   Measure the volume of the water, which is the volume of irregular object